Fourier Transforms! 2D version: model of image formation

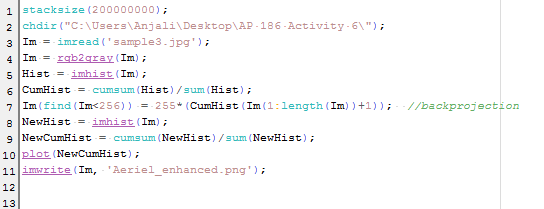
We have already encountered several applications of the Fourier transform during our Applied Physics 183 and 185 class. It is so powerful that one couldn't possibly imagine the fields of Optics and signal/image processing progressing as much as they do nowadays without it. Fourier transforms use the sum of cosines and sines in representing a certain signal. In this activity, we extend it to two-dimensional to mimic the lens of a camera as a Fourier Transformer and this it is represented by the following equation.

One property of the Fourier transform is its symmetry. The following figure schematically presents the 2-D symmetry of FT.

2D-Symmetry of FT 

ref: [2]

You will be able to observe this symmetry when we get to the result of each Fourier transformations done in this activity. 

Fourier transform can be implemented through numerical simulations. Several algorithms have been presented in solving Fourier transform, and the best one so far is the Fast Fourier Transform by Cooley and Tukey[1]. Taking in mind that Fourier transform represents a signal/image as a sum of sines and cosines, we examine the FFT of a synthetic sinusoidal image shown below:

FFT of sinusoid images along the vertical and horizontal axis

The FFT of an image of a sinusoid is relatively much simpler than other images. Its direction is also consistent with the direction of the sinusoid. Note that the FFTs shown in the figure above are zoomed-in versions for us to be able to distinguish their FFTs.

In this activity, we explore the different techniques in implementing the use of Fourier transforms in simulating an imaging device as well as editing and manipulation of images. The first part of the activity is exploring the discrete Fourier transform. We note that FFT2 best works when it's size is in the power of 2. Thus, we create synthetic images of size 128x128 in each of the applications to be explored in this activity. The first task is to create a circle of any radius. In my case, I created three with different radii and each of their FFT and shifted FFT are presented in the following figure.

FFT and shifted FFT of circles of increasing radii

The Fourier transform of an image has to be shifted because the quadrants of the image are interchanged. The resulting image is that of an Airy pattern. As the radius of the circle increases, the airy pattern decreases in size. It is interesting to  find the right radius that would result to an image of an airy pattern fit for the 128x128 px. 

I was also curious what happens if we place the circular object at the edge of a picture. Since Fourier transform detects all frequencies that appear in an image, its output is not necessarily dependent on the actual position of the signal in the image. This is demonstrated by the figure below.

The next task is to simulate an imaging device. An image of a circle represents the aperture of a camera, and the VIP image represents the object to be captured. The FFT of the object is obtained and the circular aperture is shifted. Their product is calculated the inverse is obtained to get the convolved image. The result of increasing aperture size is presented in the following figure. 

Simulation of an imaging device with increasing aperture size (circle)

The object appears more focused as the aperture size increases since the aperture is responsible for the amount of light that is captured by a lens. Simulation of an imaging device is just one of the many applications of the convolution theorem. It is what makes the use of Fourier transform very useful in the fields of Optics and image processing. The key point in this theorem is that:

Multiplication in Real Space <--->  Convolution in Fourier Space

    Convolution in Real Space <--->  Multiplication in Fourier Space

References:

[1] Maricor Soriano. A7 – Fourier Transform Model of Image Formation

[2] The Fourier Transform (What you need to know) . School of Physics, The University of Edinburgh from http://www2.ph.ed.ac.uk/~wjh/teaching/Fourier/documents/booklet.pdf Retrieved 16 July 2013

Image enhancement using histogram manipulation

The next task for our 186 lab class is image enhancement using histogram manipulation. Based from experience, we sometimes fail to set the correct settings in our camera before capturing a scene. Most of the time, (well in my case and based from my own observation and experience), it is a common mistake to take a shot that is dark. There is a certain threshold to which our eyes is sensitive to. In this activity, we can enhance dark images to be able to see more detail about the picture.

I chose the following image of Aeriel during her mock wedding with Nestor last February. As you can see, the image is dark and the objects in front of Aeriel are not clear. Now, suppose we want to enhance the image to make it look brighter and more detailed, we could just manipulate the grayscale PDF of the original image by backprojecting the grayscale values of a desired cummulative distribution of grayscale values.

Image to be enhanced

The first step is to get the cumulative histogram (CDF) of the grayscale values of the image and use it to backproject values from the desired one. The CDF of a normal probability distribution function is that of a constant. So in enhancing our image, our goal is to normalize as much as possible the histogram of our image.  The following image shows the original and the enhanced CDF of our image.

As observed, the highest pixel value present in the original image is only about 100 pixels, which is why the image is generally dark.  Recall that in a grayscale image, the brightest pixels are at 255 px. I started by converting a given RGB image into grayscale and plotted its histogram. I then proceeded to computing its CDF and as already mentioned, the result is shown in the left side of the above picture. 

Using the  original and the desired CDFs, the pixel values of the grayscale image is replaced. I remember our 185 class and thought about the input-output curve of a system. In this case, the I-O curve is the desired CDF.

I was not really familiar with the matrix operations here in Scilab and I first opted in using for loop. But then my code was not working and for some reason I couldn't find the bug. Aside from the fact it is slow and faulty, it was not elegant. So then Joshua thought me with the one-line code. I didn't know that Scilab allows operations in each element of a matrix to be done simultaneously. Although the idea is the same, mine was broken down to for loop, where the operation is performed to each element one at a time. I was amazed when I found out that Scilab could handle a matrix operation as one. Indeed, it could be the best tool for image processing.

Finally, I produced the following enhanced image:

Wondering what happened to the histogram of the enhanced image? Here:

Histogram of the enhanced image

Observing it closely and comparing it to the original histogram, I realized that the the points were just basically spread out through the 1-255 range. It was made to follow the normal distribution. Its cumulative distribution is quite more interesting since it wasn't able to follow an exactly straight line. Shown below is the CDF of the enhanced image and the desired (straight line).

CDF of the enhanced image

This method here can also be done without using Scilab. Other free and more user-friendly software are available online. One example is the GIMP. We can use GIMP to manipulate the histogram of a given image the same way we did using Scilab. Now loading the same image in GIMP and following Image > Mode> Grayscale and then Color > Curves, we can adjust the color curves of the image by choosing the preferred input-output curve. In our method using Scilab, we chose a constant line as our I-O curve. A snapshot of the manipulation using GIMP is shown below:

Histogram Manipulation using Color Curve in GIMP (Grayscale)

One also has the option to do this without converting the image to grayscale. The different channels red, green and blue can be manipulated individually as can be seen from the snapshot below:

Histogram Manipulation using Color curve in GIMP (RGB)

This technique can also be done by using other softwares like Photoshop. Here one can simultaneously view the resulting histogram of the image as you vary the I-O response curve. The picture below shows a snapshot of the Curve and the Histogram of the same image loaded to Photoshop.

Histogram Manipulation using Photoshop

Indeed, there are a lot of techniques available in enhancing an image. It is interesting to understand how these software work. Behind their user-friendliness is a deep information that only lucky students like us can be able to understand. For this activity, I give myself a grade of 11/10 for doing all the required work and for further exploring other software. I am looking forward to the next activities. :)